Bitcoin Proof of Work

(With try yourself code!)

As much as bitcoin (note here I’m talking about the software also known as bitcoin core) is a highly complex system many of the basic elements can be fairly easily described and demonstrated.

Here I’ll demonstrate a very simple example using python showing how mining works and how something called ‘difficulty’ is controlled.

But first we need some background.

Mining (New Blocks)

One of the most important elements is the process of mining that in turn adds new blocks to the blockchain but also creates newly minted Bitcoin.

Mining is where computers basically race each other to solve a mathematical problem. If they solve it first they create a new block of transactions on the blockchain and are rewarded with newly minted Bitcoins.

What is the Block Reward?
The amount that miners may claim as a reward for creating a block.

https://bitcoin.org/en/glossary/block-reward

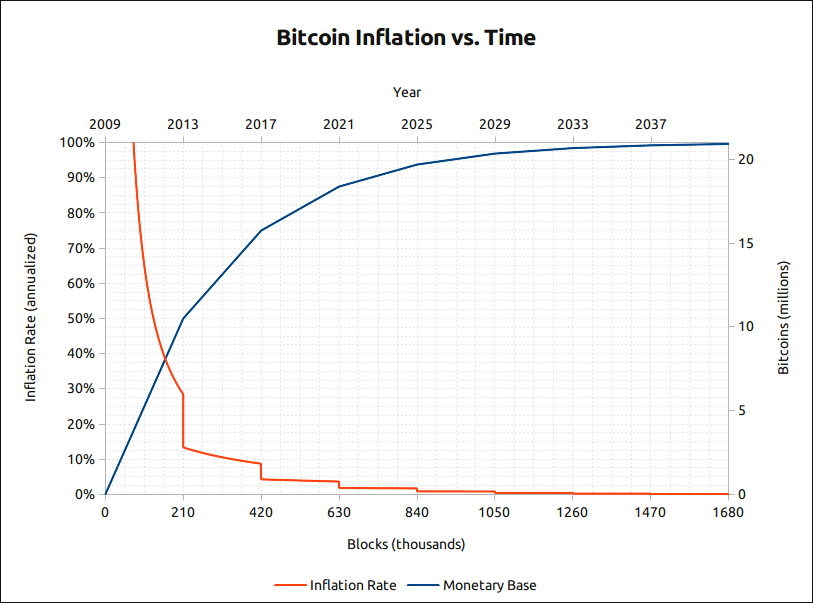
These new Bitcoins are known as the Block Reward which coincidently is big news right now as this reward is due to be cut in half on May 12th. This event, known as the Halving, occurs every 210000 blocks which translates to every 4 years or so.

But back to the miners.

The problem they need to solve is actually simple to explain but hard to solve. They take a group of transaction hashes and hash them together along with a random variable (called a nonce). This is shown below.

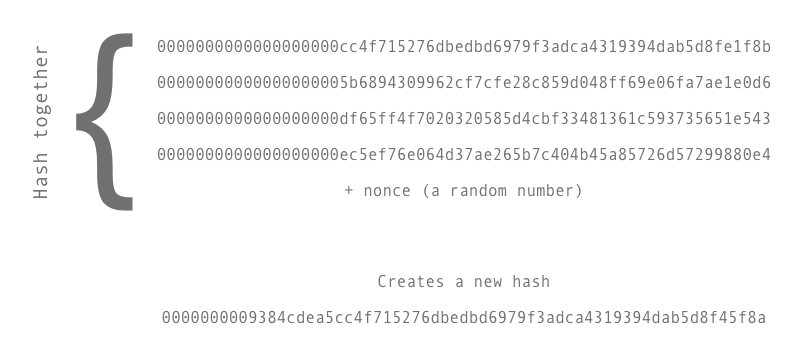
The trick is that the Bitcoin software controls the difficulty by telling the miners that the hash they need to produce must start with at least a minimum number of zeros (target hash).

Since the hashes generated are completely random the only way to generate a hash with the required number of zeros is to keep adding different random number to the original hash and try again.

What is Hashing?

In simple terms, hashing means taking an input string of any length and giving out an output of a fixed length. In the context of cryptocurrencies like bitcoin, the transactions are taken as input and run through a hashing algorithm (bitcoin uses SHA-256) which gives an output of a fixed length.

https://blockgeeks.com/guides/what-is-hashing/

The magic of hashing is that it’s a one way process and output cannot be predicted from the input, meaning brute force computing is the only way to get the required output hash. There are no shortcuts.

The other benefit of hashing is that although they are hard to generate they can be very easily verified afterwards using almost no computing power. So my laptop can verify a miner has created a valid block with a valid hash in microseconds.

Hashing is a type of Trapdoor function since it is easy to go from input to hash but impossible to get the original input from the hash.

How does the difficulty adjust over time?

Bitcoin is programmed to generate new blocks every 10 minutes on average. A predictable supply.

In the early days the computing power used for mining was minimal so the difficulty to produce a block was relatively easy and only a few zeros were required for a valid block.

As the years have passed more and more miners come onboard with more and more powerful equipment. If the difficulty didn’t adjust new blocks would be created too fast and the average block time would be far below 10 minutes.

This would also mean the total supply (capped at 21 million bitcoin) would be minted almost immediately.

The elegance of mining and difficulty retargeting is that every 2016 blocks (about every 2 weeks) the code self adjusts the difficulty so if blocks are being mined too fast the difficulty increases, meaning miners now have to calculate hashes with more leading zeroes.

Conversely if mining power leaves the network the opposite happens. Blocks are mined too slowly so after 2016 blocks the difficulty is adjusted downwards and fewer leading zeros are required on hashes.

OK, I Need a Demonstration 🤯

To demonstrate the mining process we can use some fairly simple python code.

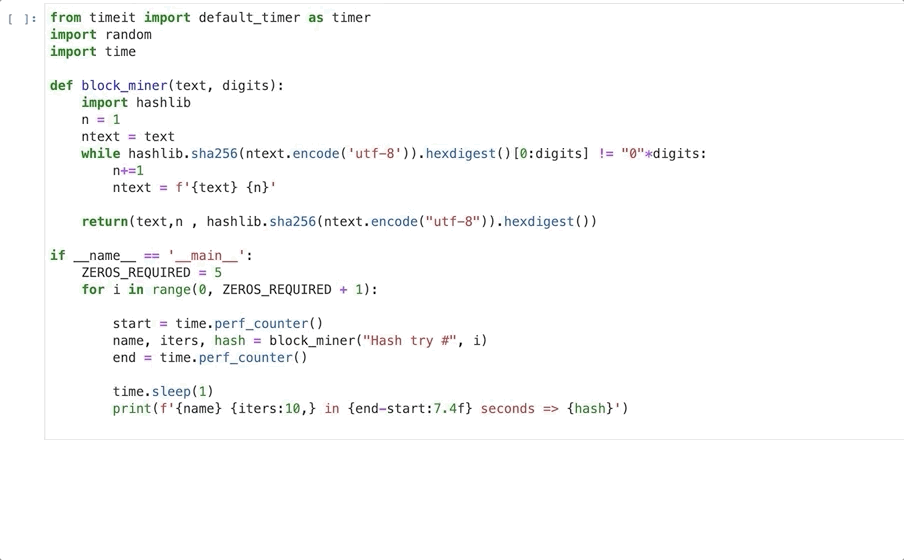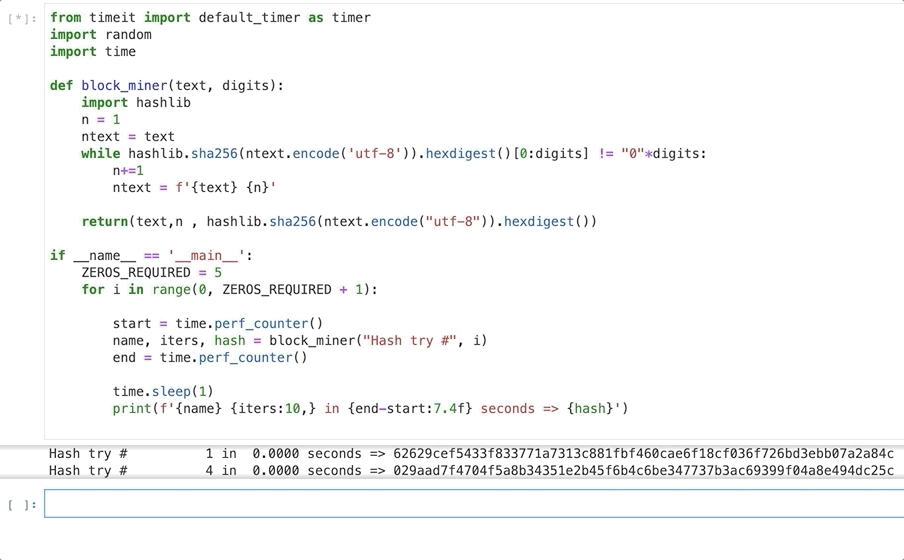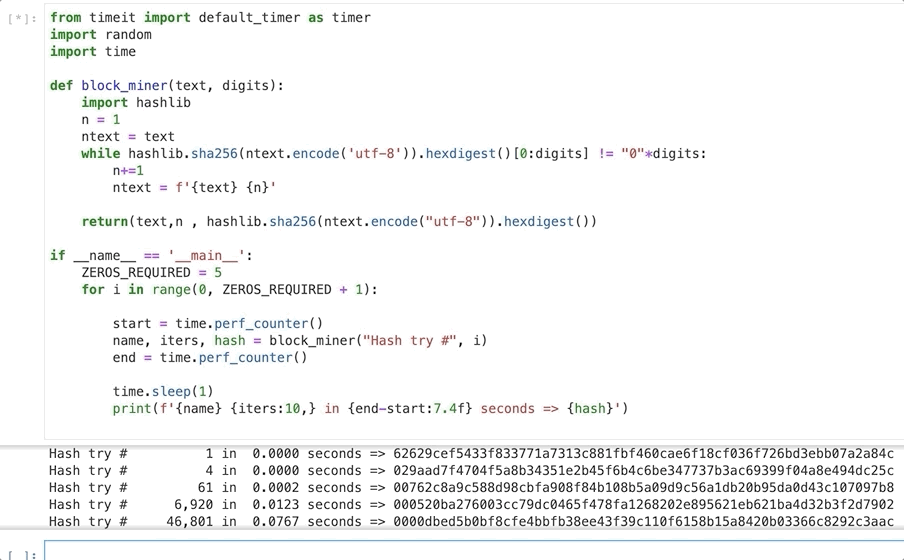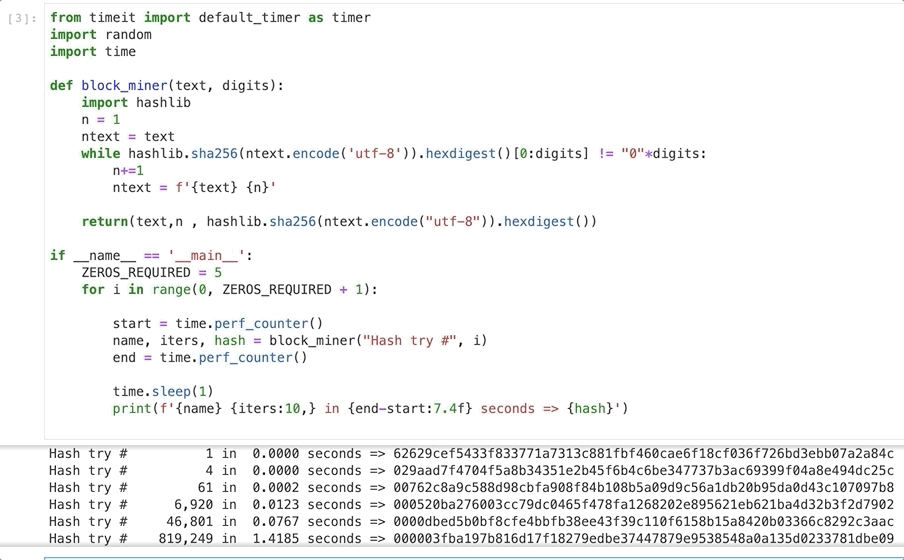
This code runs 6 loops with increasing difficulty starting with a target hash with no zeros and ending with 5. Within each difficulty it calculates a hash that matches the target hash and outputs the number of iterations required, the time taken and the hash produced.

The initial input is a text string, in this case ‘Hash try #’.

Next it creates a hash of the text and checks if the hash has the required number of leading zeros. If it does we print the output and hash and then try again but on the next loop the required zeros (target hash) increased by one.

If the hash doesn’t meet our difficulty we add a digit to the input text, hash this and test again. This loop continues until we finally get an output hash that meets our target hash.

Difficulty Increases Rapidly!!

As you can see creating a hash with one leading zero is trivially easy even on my laptop. Even three leading zeros only takes 0.012 seconds.

But things really change rapidly as we increase the difficulty so at 5 leading zeros it takes 1.45 seconds and over 800.000 iterations.

On my Macbook Pro generating a hash with 6 leading zeros took 64 seconds and over 44 million iterations.

I finally tried to generate a hash with 7 leading zeros:

Hash try # 675,193,594 in 952.3370 seconds => 000000096a22c89e6d0a2f1ea37719f8546aac9becfaf1e7875983f6df35adfa

After 675 million iterations and almost 16 minutes the target hash was found!

The current difficulty as of today requires 19 leading zeros and miners calculate 117 Exahashes per second (one Exahash is 1.000.000.000.000.000.000 or a million million million)

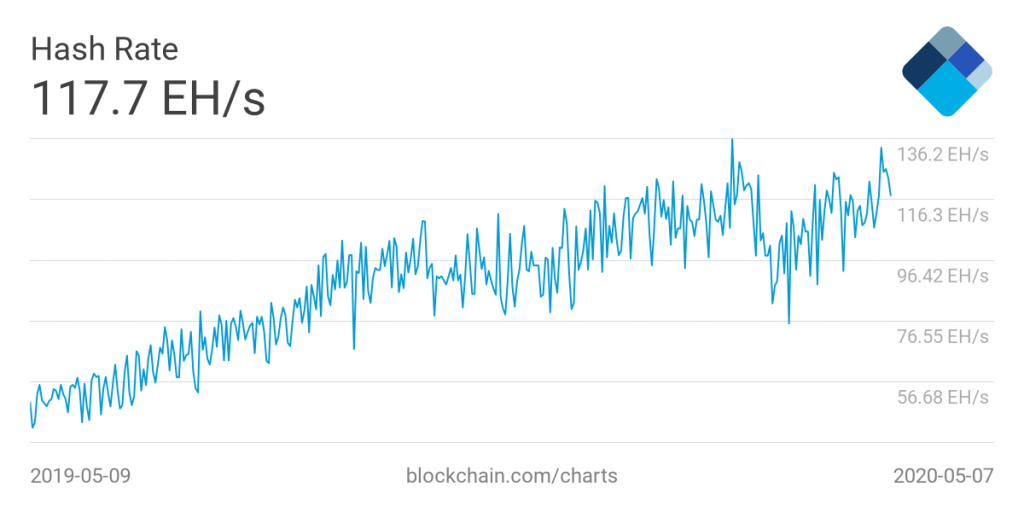
This explains why mining on regular computers is no longer possible and dedicated hardware is required located in places where electricity is cheap.

The Code

If you just copy this code and run you can try for yourself. Try adjusting the variable ZEROS_REQUIRED to another integer to change the hash target.

You can also try with a different input text by editing “Hash try #” and changing it to any text you like.

from timeit import default_timer as timer
import random
import time

def block_miner(text, digits):
    import hashlib
    n = 1
    ntext = text
    while hashlib.sha256(ntext.encode('utf-8')).hexdigest()[0:digits] != "0"*digits:
        n+=1
        ntext = f'{text} {n}'
    
    return(text,n , hashlib.sha256(ntext.encode("utf-8")).hexdigest())

if __name__ == '__main__':
    ZEROS_REQUIRED = 6
    for i in range(0, ZEROS_REQUIRED + 1):
        
        start = time.perf_counter() 
        name, iters, hash = block_miner("Hash try #", i)   
        end = time.perf_counter()  
        
        print(f'{name} {iters:10,} in {end-start:7.4f} seconds => {hash}')

One of the amazing aspects of bitcoin is that everything is controlled algorithmically and can be independently validated by anyone. If you run a bitcoin node you can see every transactions and validate them for yourself if you wish.